Betrachten wir noch einmal folgende Grafik der Halbwertszeit:
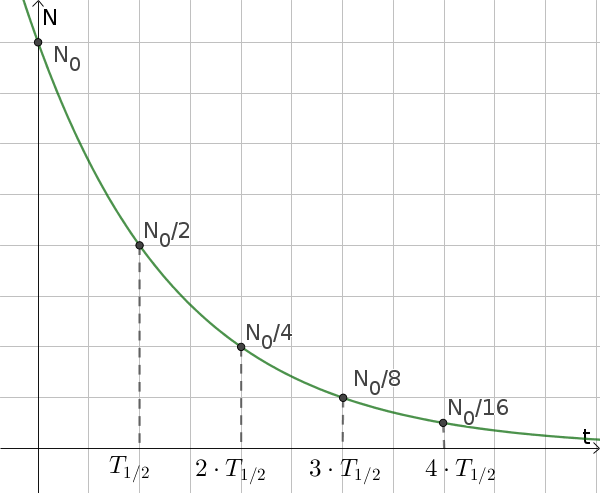
Die Zahl der unzerfallenen Kerne lässt sich nun abhängig von der Zeit darstellen:
| Zeit $t$ | Anzahl Kerne $N(t)$ |
|---|---|
| $t=0$ | $N_0$ |
| $t=1\cdot T_{1/2}$ | $\frac12\cdot N_0$ |
| $t=2\cdot T_{1/2}$ | $\frac14\cdot N_0$ $=(\frac12)^2\cdot N_0$ |
| $t=3\cdot T_{1/2}$ | $\frac18\cdot N_0$ $=(\frac12)^3\cdot N_0$ |
| $t=4\cdot T_{1/2}$ | $\frac1{16}\cdot N_0$ $=(\frac12)^4\cdot N_0$ |
| $...$ | $...$ |
| $t=\color{blue}{n}\cdot T_{1/2}$ | $(\frac12)^\color{blue}{n}\cdot N_0$ |
Jetzt stellen wir $t=n\cdot T_{1/2}$ noch nach $n$ um:
Eingesetzt für $n$ erhalten wir schließlich folgende Gleichung abhängig von $t$: